- 擴散硅壓力變送器
- 電容式壓力變送器
- 無紙記錄儀
- HART手操器
- 溫度儀表
- 溫度變送器
- 石英管液位計
- 浮球液位計
- 電容式液位計<
- 射頻導納液位計
- 雷達物位計
- 壓力源
- 安全柵
- 壓力表
- 精密數字壓力表
- 溫度校驗儀
- 流量計
- 孔板流量計
- 彎管流量計
- 威力巴流量計
- 橢圓齒輪流量計
- 渦輪流量計
- 金屬管轉子流量計
- 超聲波流量計
- 玻璃轉子流量計
- 旋進漩渦流量計
- 錐形流量計
- 液體流量計
- 氣體流量計
- 風壓變送器
- 壓力負壓變送器
- 小巧型不銹鋼壓力變送器
- PT100鉑熱電阻
- 投入式靜壓液位變送器
- 防腐投入式液位變送器
壓力變送器介紹非線性振動的基本特性
前面壓力變送器介紹的動力計算中提到一個方程如圖1所示。在這個方程中,慣性力、阻尼力和彈性力均為線性、常系數的.應用這個方程能夠解決許多實際的問題.但是機械系統振動(riIJ題中有許多現象無法用線性振動理論來解釋。例如。由于大位移而導致的幾何非線性。或由于限尼力、彈簧力的因素產生的物理非線性。這類問題的運動方程是非線性的,故稱為I卜線性振動問題。
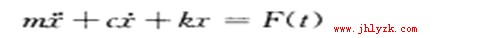
引起非線性振動的原因很多。主要是非線性恢復力和非線性阻尼力所致。
非線性恢復力(弓單性力)是指彈性元件材料的力與變形不成線性關系或山于JL何構造原因造成的恢復力與位移的關系不成線性.非線性Pit尼力則說明某些振動系統中復雜的阻尼不能通過前面所述簡化方式線性化處理。
非線性振動有許多一與線性振動完全不同的從本性質,現擇要簡單介紹如下.
I)振動傾率隨振幅變叮匕
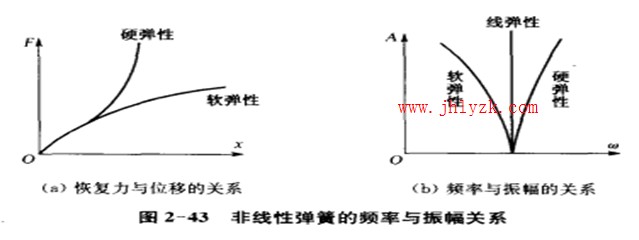
恢復力為非線性時,系統的tAi有頻率隨振福的大小而變化.壓力變送器發現這與線性系統固有頻率f義與系統參數有關的性質完全不同。如非線性彈性為硬彈性(彈性系數隨位移增大而提高)。Nut頻率陸振幅增大而提高;反之,如為軟彈性。則傾率隨振幅增大而減"1",圖2-43所示為非線性彈簧的變形一恢復力關系和且有非線性恢復力系統的頻率一振幅關系。
則振幅又將從C點升到d點。又發生一次突變。然后再助板率的減小而趨向于樸位移依.對于軟彈性的非線性系統.也會發生類似的現象.

非線性受迫振動中振幅肋激振力頗率變化而發生的這種突變現象稱為跳躍現象。在激振領率由小到大漸變和由大到小漸變時。探幅變化的過程不4411-1.這些現象在線性振動系統.書,是不會發生的。
3)次玄咨名吸動和超i啼才長動
一個線性的機械系統。在簡t皆激振力Fsin的作用下。它的受迫報動僅包含傾率為.的諧波響應.當激振力孩率。接近系統固有頻率二時。系統只出現與干擾力頻率相I司的共振.但對于非線性機械系統而言。情況就不同。在簡i許力Fsin作用下。系統的受迫振動
不僅包含頻率為。的諧波響應,還會有傾率為號的次諧波響應和預率為”.的妞諧波響應《為正整數).系統中究竟會發生哪些次i皆振動和超諧振動。耍視具體條件而定.由于次i片和超i桿振動的存在,非線性系統中除了會發生激振傾率.接近于系統固有狽率.。的i片波
共振外,還會發生。.的超諧共振或譽的次1W共振·因此·非線性系統的響應頗率數目超過了系統的門山度數目。較之線性系統有更多的發生共振的可能性.
4)女且合奴率振動
非線性系統受到兩個以上械率簡活力激振時。會產生組合領率的受迫振動.設系統受到兩個簡i鑄千擾力廠和Fxxin的作用,則系統不僅可能有傾率為。以及粉贊的受迫振動響應,還會出現毅率為組合頗率動兒中。差壓變送器計算他們的和為正枯數。
5》疊加原理不適用
線性系統中可川登加原理處理問題。即系統在多個激掀力作用卜的響應可認為是各個激振力單獨作用下系統響應的柱加。
由非線性系統的組合傾率振動現象可知,對于非線性系統而言。畏加原理已不再適用。
求非線性系統的全解不能像求線性系統的全解那樣。由求得的各個特解處加而成。系統對多個激振的響應井不是簡單地對梅個激振響應的柱加。而是對這些激振的綜合響應。這種情況使得尋求非線性系統的全解變得份分復雜。
2)跳躍現象
具有非線性彈性的機械系統。在簡i片激振強迫振動時。它的幅頓曲線不同于線性系統。曲線有向右(硬彈性時)或向左(軟彈性時)杏曲的現象,如圖2-44所示。
對線性系統而言,激振力輻俏保持不變而逐漸改變激振力的頻率時,不論是頻率值由小到大變化,還是由大到小變化,系統受迫振動幅仇的變化都是連續的〔見圖2-44(a)]。但楚. R"r于非線性系統。以硬彈性為例〔見圖2-44(c)].當激振力輻位不變而逐漸增加激振力頗率時,振幅也隨著增大。在振幅增大到“點后。再增大頻率則振幅將突然從“點降到b點。發生一個突變。如頻率是從高頻向低頻變化,則振幅變化將沿be到達c點,再繼續減低傾
下一篇:機械振動的定義與表示方法
上一篇:液壓傳動的工作原理
- 2019-1-17
 磁翻板液位計使用原理及使用注意事項
磁翻板液位計使用原理及使用注意事項 - 2017-7-3
 靜壓液位計從眾多液位計當中脫穎而出的...
靜壓液位計從眾多液位計當中脫穎而出的... - 2017-6-30
 壓力變送器選型指南和技術支持
壓力變送器選型指南和技術支持 - 2016-11-9
 壓力變送器的應用領域有哪些?
壓力變送器的應用領域有哪些? - 2016-10-24
 儀器儀表行業將向智能化方向發展
儀器儀表行業將向智能化方向發展
- 2019-1-25
 火電廠化學水處理液位計的發展之路
火電廠化學水處理液位計的發展之路 - 2019-1-21
 磁翻板液位計:儀器儀表界的“新貴”
磁翻板液位計:儀器儀表界的“新貴” - 2018-11-26
 將對差壓變送器零點遷徙成績停止詳細的...
將對差壓變送器零點遷徙成績停止詳細的... - 2018-11-24
 當差壓變送器用于蒸汽等溫度較高的物資...
當差壓變送器用于蒸汽等溫度較高的物資... - 2018-11-23
 慣例辦法對智能變送器停止校準是不行的
慣例辦法對智能變送器停止校準是不行的